Present Value and Bond Pricing Fundamentals

If someone promised to give you $105 one year from now, how much would that be worth today? This simple question is about Present Value (PV) — one of the most fundamental concepts in finance. It appears frequently on bond pricing questions and is essential for many areas of the CFA Level I exam.

In this article, I’ll explain how PV calculations apply to bond pricing.

What is Present Value?

Present Value (PV) answers a simple question: How much would someone pay you today in exchange for a payment — or stream of payments — you’re promised to receive in the future?

This concept lies at the heart of financial valuation. If you’re preparing for the CFA Exam, you’ve probably heard of the time value of money — meaning a dollar today is worth more than a dollar tomorrow.

You need to fully understand the basic bond pricing concepts covered here. These are building blocks for virtually everything else you’ll encounter in fixed income analysis, not only in Level I but also Levels II and III.

Let’s start by answering our opening question:

If you’re promised $$ 105$ one year from now, and the current interest rate is $5 %$ , then the present value of that $$ 105$ is:

$P V = \frac{105}{1 + 0.05} = 100$

This means the price RIGHT NOW for this future payment is $$ 100$ . That $$ 100$ is the present value of the $$ 105$ future payment.

This is our basic formula for calculating Present Value for a SINGLE cash flow.

P V = \frac{F V}{(1 + r)^{N}}

Present Value of a Single Cash Flow

Where:

$P V$ = Present Value
$F V$ = Future Value
$r$ = Discount rate (required rate of return)
$N$ = Number of periods

CFA Level I introduces Present Value early, in the 2nd learning module of Quantitative Methods called “Time Value of Money”. Today we focus on this particular Learning Objective:

Learning Objective

Quantitative Methods | Time Value of Money

calculate and interpret the present value (PV) of fixed-income and equity instruments based on expected future cash flows

To keep things manageable, we’ll focus only on fixed-income for now.

Present Value in bonds (zero coupon case)

As we established, Present Value is the current value of future cash outflows. This relates directly to the current prices (present values) of bonds. A bond’s current price equals the current value of all its future cash outflows. For every payment a bond promises, we can calculate its present value, add them together, and determine the bond’s price.

A bond’s promised cash flows can include two components:

Regular coupon payments (PMT)
The par value (face value, principal) repaid at maturity

Each cash flow is discounted at the market discount rate (or yield to maturity, YTM). YTM reflects the return required by investors — it shows how much investors “discount” future cash flows.

We can perform two types of calculations:

The simplest involves zero-coupon bonds (discount bonds). These bonds make no periodic payments and only promise to pay par value at maturity. This is exactly like our first example — valuing $$ 105$ received in the future. We had only one year, but imagine waiting multiple years with compounding effects in the discount.

For zero-coupon bonds, calculating PV is straightforward: the price reflects only the present value of the bond’s par value.

The bond trades at a deep discount to par because you only receive a single payment at maturity. Investors earn returns purely from the difference between the discounted price paid today and the face value received at maturity.

If a 10-year zero-coupon bond promises to pay $1,000 at maturity and the market discount rate is 5%, its present value is:

$P V = \frac{1000}{(1 + 0.05)^{10}} = 613.91$

Thus, you’d pay about $614 t o d a y t o r e c e i v e$ 1,000 in 10 years — earning returns entirely from price appreciation.

Present Value in bonds (coupon case)

The second option is a bond that pays both par value (FV) at maturity and coupon payments (PMT) during the bond’s life.

For a bond with N periods to maturity, periodic coupon payment C (if paid annually, C = coupon rate × face value), face value F (par value paid at maturity), and discount rate per period r (YTM per period), the present value (price) can be written as:

P V = \sum_{t = 1}^{N} \frac{P M T}{(1 + r)^{t}} + \frac{F V}{(1 + r)^{N}}

Present Value of a Coupon Bond

This formula simply adds the discounted value of each coupon payment plus the discounted face value.

If coupons are annual and YTM is an annual rate, use years for t. If coupons are semiannual (twice per year), adjust r to the semiannual YTM (e.g., YTM/2) and let N be the total number of semiannual periods.

Let’s use simple numbers for a hand calculation.

Given:

Par Value (FV) = $$ 100$
Coupon Rate = $4.75 %$ → PMT = $$ 4.75$ annually
Maturity = 3 years → $N = 3$
Yield to Maturity (YTM) = $6.00 %$ annually → $r = 0.06$

We want to calculate the present value (price) of this bond.

Solving the Bond Pricing Problem with Coupon Bonds

Step 1

Break down the cash flows:

The bond pays:

$4.75 at the end of Year 1
$4.75 at the end of Year 2
$4.75 + $100 = $104.75 at the end of Year 3

Step 2

Discount each cash flow.

It just means we need to calculate the PV of coupon payments and principal payment.

$P r i c e = \frac{4.75}{(1.06)^{1}} + \frac{4.75}{(1.06)^{2}} + \frac{104.75}{(1.06)^{3}}$

$P r i c e = \frac{4.75}{1.06} + \frac{4.75}{1.1236} + \frac{104.75}{87.96}$

Step 3

Sum the components - calculate overall PV

$P r i c e = P V_{c o u p o n s} + P V_{p r i n c i p a l}$

$P r i c e = 4.48 + 4.23 + 87.96 = $ 96.67$

Here’s a simple tip that can sometimes give you the answer without detailed calculations:

When the coupon rate is lower than YTM, the bond pays less interest than the market requires. In this situation, the bond will always trade at a discount — below par value $(P V < F V)$ .

In the opposite situation, when the bond pays more interest than the market requires, the bond price will be above par value.

Another important relationship: under the same bond conditions (YTM, par value), more frequent payments (for example, semiannually) will result in a higher current price (PV). For example, a 5% annual coupon paid semiannually (2.5% every 6 months) means you receive some interest sooner and can reinvest it. This benefits you, so the bond price won’t be as discounted as an annual payment bond with the same 5% coupon rate.

Key Insight: The Inverse Relationship

Bond prices and yields move in opposite directions. When interest rates (yields) rise, bond prices fall, and vice versa. This is because:

Higher yields → Higher discount rates → Lower present values → Lower bond prices
Lower yields → Lower discount rates → Higher present values → Higher bond prices

This relationship is non-linear and becomes more pronounced for bonds with longer maturities.

Financial Calculator Tutorial

The CFA Institute only allows two types of calculators during the exam: Texas Instruments® BA II Plus™ and HP® 12C.

If you’re starting fresh, the TI BA II Plus is the recommended choice. It’s widely supported, intuitive, and used throughout CFA prep resources.

Essential Calculator Keys

To solve nearly any present value or bond pricing question on the exam, you need to know these five keys:

N = Number of compounding periods
I/Y = Interest rate per period (in % form, not decimal)
PV = Present Value (today’s price or value)
FV = Future Value (final lump sum, like bond par value)
PMT = Payment per period (like bond coupons)

Using the Calculator

To help you practice CFA-style problems, I’ve built a Time Value of Money Calculator that works just like the exam-approved financial calculators.

How to use it?

Step 1: Enter values for any four of the five fields Step 2: Leave the one you want to calculate blank Step 3: Press the compute key for the unknown variable

Example inputs for our zero-coupon bond:

Bond Price in Zero Coupon Bond

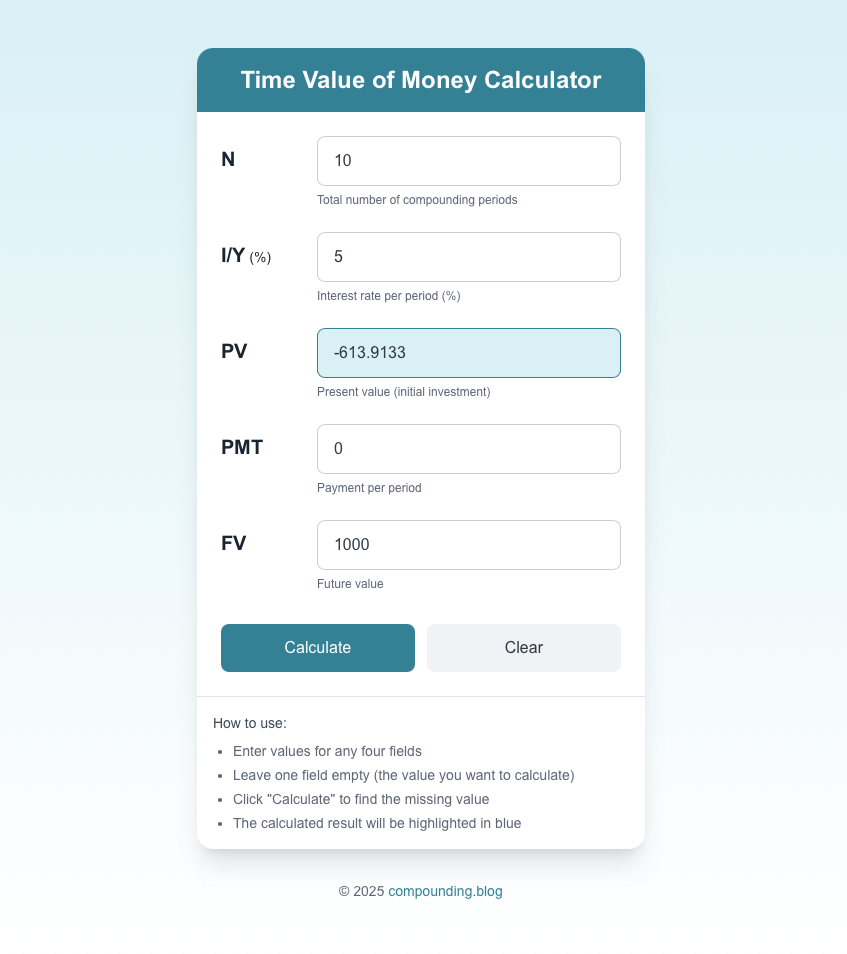
Example inputs for our coupon bond:

Bond Price in Coupon Bond

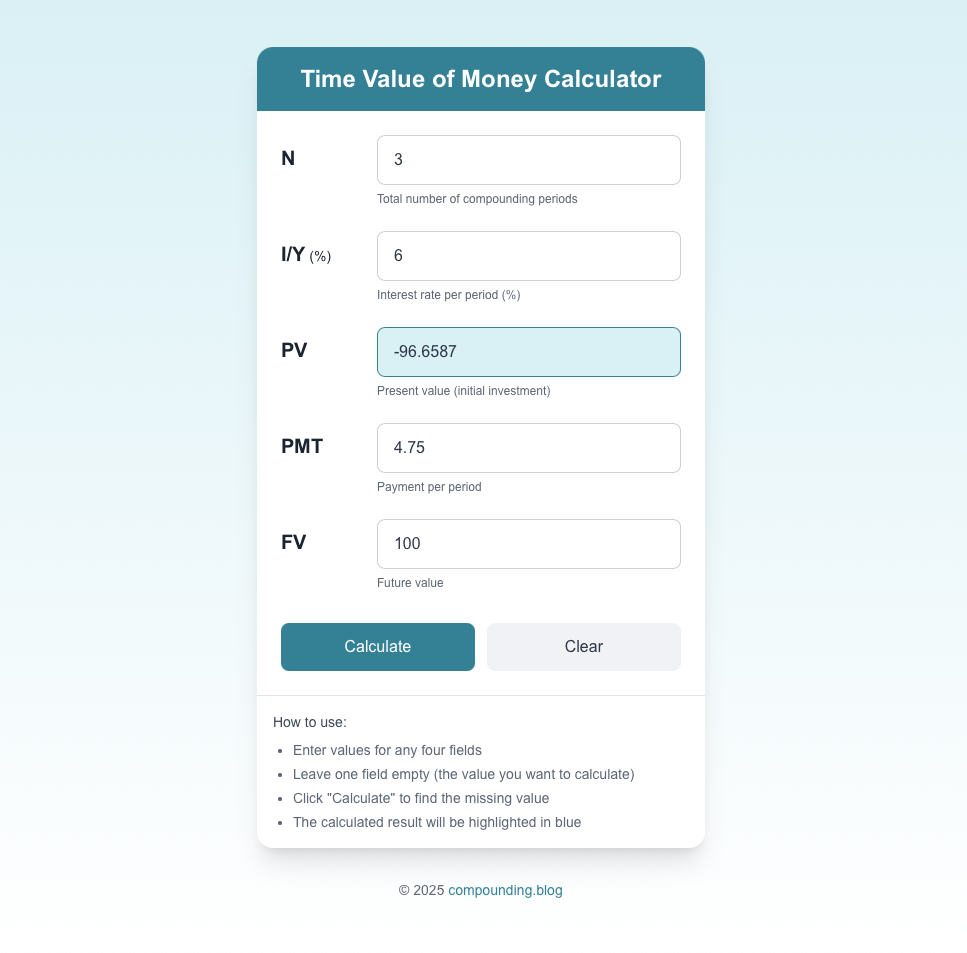
Understanding Cash Flow Signs

When using any financial calculator, cash inflows and outflows must have opposite signs:

PV usually represents a cash outflow — money you invest today (e.g., buying a bond)
PMT and FV are usually inflows — money you receive (coupon payments and principal)

If you enter PMT = 4.25 and FV = 100, your calculator treats these as inflows and returns PV as negative (e.g., PV = -97.96).

This minus sign simply reflects cash flow direction: you paid 97.96 to receive 4.25 + 100 in the future.

Today’s Challenge

Let’s finish this article with a simple CFA-like problem:

Problem

Five years ago, a corporation issued a 15-year zero-coupon bond with a face value of $1,000. The bond is currently trading at $472.58. Assuming annual compounding, the bond's market yield to maturity (YTM) is closest to:

A) 6.2%

B) 6.7%

C) 7.8%

What we know:

Face value (FV) = $1,000
Current price (PV) = $472.58
Time remaining = 15 – 5 = 10 years → N = 10
PMT = 0 (zero-coupon bond = no periodic payments)
We’re solving for: YTM = ? (I/Y)
Compounding is annual, so we don’t need to adjust frequency

This is a classic present value of a lump sum problem:

Solving the Bond Pricing Problem with Zero Coupon Bonds

Step 1

Break down the cash flows:

We have a zero-coupon bond with only one cash flow at maturity. The key is calculating the time remaining correctly: we’re interested in the current price (today, 5 years after issuance) and need the YTM for the remaining 10 years to maturity.

Cash flow:

$1,000 at the end of Year 10 (from today)

Step 2

Discount each cash flow.

Set up the present value equation:

For a zero-coupon bond, we only discount the principal payment:

$P V = \frac{F V}{(1 + r)^{N}} = \frac{1000}{(1 + r)^{10}}$

Step 3

Solve for YTM (r):

$472.58 = \frac{1000}{(1 + r)^{10}}$

$(1 + r)^{10} = \frac{1000}{472.58} = 2.116$

$1 + r = (2.116)^{\frac{1}{10}} = 1.078$

$r = 0.078 = 7.8 %$

If you use my calculator here are the needed inputs:

Bond Price in Zero Coupon - Calculator

Problem

A) 6.2%

B) 6.7%

C) 7.8%

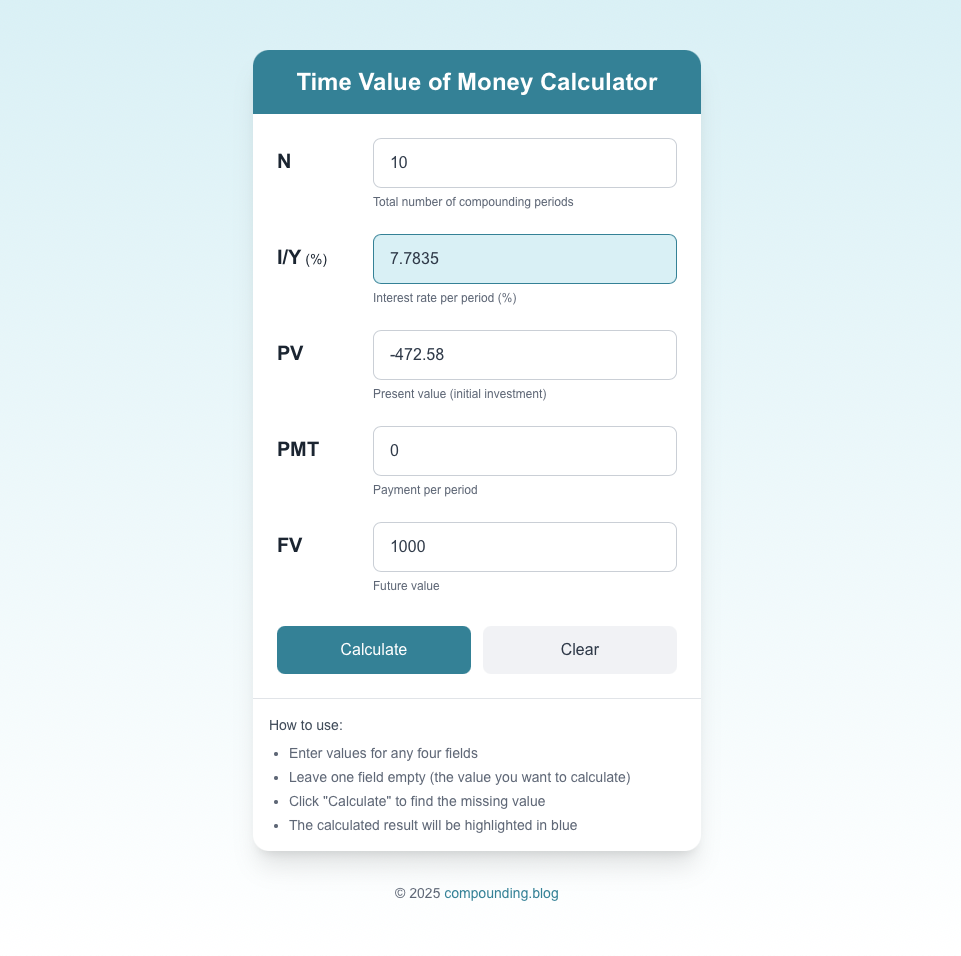
Semi-Annual Compounding

Here’s where many CFA candidates make mistakes: most bonds pay coupons semi-annually, not annually. This significantly affects calculations.

Key Adjustments for Semi-Annual Bonds

When bonds pay semi-annually, you must adjust three variables:

Coupon payment = (Annual coupon rate × Face value) ÷ 2
Number of periods = Years to maturity × 2
Periodic yield = Annual YTM ÷ 2

Example: Semi-Annual Bond Pricing

Let’s work through a complete example:

Given:

Face value: $1,000
Annual coupon rate: 6%
Time to maturity: 4 years
Annual YTM: 8%

Convert to semi-annual terms

Semi-annual coupon payment: (6% × $1, 000) \div 2 =$ 30
Number of periods: 4 years × 2 = 8 periods
Semi-annual yield: 8% ÷ 2 = 4% per period

Solving the Semi-Annual Bond Pricing Problem

Step 1

Break down the cash flows:

The bond pays:

$30 at the end of Period 1 (6 months)
$30 at the end of Period 2 (1 year)
$30 at the end of Period 3 (1.5 years)
$30 at the end of Period 4 (2 years)
$30 at the end of Period 5 (2.5 years)
$30 at the end of Period 6 (3 years)
$30 at the end of Period 7 (3.5 years)
$30 +$ 1,000 = $1,030 at the end of Period 8 (4 years)

Step 2

Discount each cash flow.

We need to calculate the PV of each coupon payment and the principal payment:

$P r i c e = \frac{30}{(1.04)^{1}} + \frac{30}{(1.04)^{2}} + \frac{30}{(1.04)^{3}} + \frac{30}{(1.04)^{4}} +$ $\frac{30}{(1.04)^{5}} + \frac{30}{(1.04)^{6}} + \frac{30}{(1.04)^{7}} + \frac{1, 030}{(1.04)^{8}}$

$P r i c e = \frac{30}{1.04} + \frac{30}{1.0816} + \frac{30}{1.1249} + \frac{30}{1.1699} +$ $\frac{30}{1.2167} + \frac{30}{1.2653} + \frac{30}{1.3159} + \frac{1, 030}{1.3686}$

Step 3

Sum the components - calculate overall PV

$P r i c e = 28.85 + 27.74 + 26.67 + 25.64 +$ $24.65 + 23.70 + 22.79 + 752.63 = $ 932.67$

Bond Price vs. Yield Relationships

Premium Bond: Coupon rate > YTM → Price > Par value
Par Bond: Coupon rate = YTM → Price = Par value
Discount Bond: Coupon rate < YTM → Price < Par value

Wrapping Up

Present value is the foundation upon which most financial analysis rests. Whether you’re valuing bonds, stocks, or capital projects, you’re essentially asking: “What is this stream of future cash flows worth today?”

Master these concepts, and you’ll find that many seemingly complex CFA problems become much more manageable.

See you soon!

What is Present Value?#

Learning Objective

Present Value in bonds (zero coupon case)#

Present Value in bonds (coupon case)#

Solving the Bond Pricing Problem with Coupon Bonds

Financial Calculator Tutorial#

Essential Calculator Keys#

Using the Calculator#

Understanding Cash Flow Signs#

Today’s Challenge#

Solving the Bond Pricing Problem with Zero Coupon Bonds

Semi-Annual Compounding#

Key Adjustments for Semi-Annual Bonds#

Example: Semi-Annual Bond Pricing#

Solving the Semi-Annual Bond Pricing Problem

Wrapping Up#

What is Present Value?

Present Value in bonds (zero coupon case)

Present Value in bonds (coupon case)

Financial Calculator Tutorial

Essential Calculator Keys

Using the Calculator

Understanding Cash Flow Signs

Today’s Challenge

Semi-Annual Compounding

Key Adjustments for Semi-Annual Bonds

Example: Semi-Annual Bond Pricing

Wrapping Up